 |
|
|
|
|
|
|
Monte Carlo Integration
To find the area under a curve, one can use integral calculus. If the curve has
no close form, such as the normal curve, then the area can not be derived
analytically. However, with today's computer technology, one can use Monte Carlo
Integration to achieve such task. The area under a distribution is also known as
probability. In this example, we want to compute the area under standard normal
probability distribution from 0 to z.
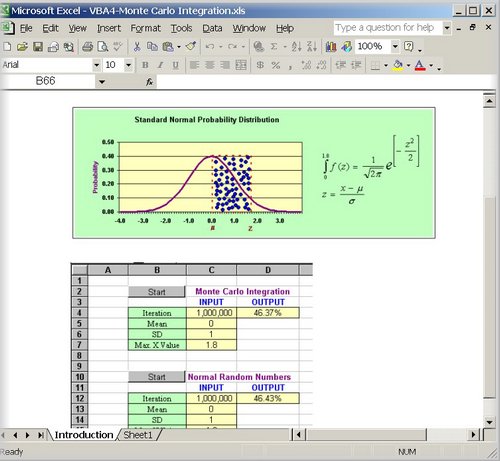
See Examples below;
Standard Deviation and Mean
>
Lotto Number Generator
>
Playing Card
Probability
>
Normal Distribution Random Number Generator
>
Monte Carlo Integration
>
Black-Scholes Option Pricing Model - European Call and Put
>
Binomial Option
Pricing Model
>
Portfolio Optimization
>
Multiple Regression
>
Bootstrap - A
Non-Parametric Approach
>
Multivariate Standard Normal Probability Distribution
>
Monte Carlo Simulation
>
Option Greeks Based on Black-Scholes Option Pricing Model.
$29.95
Payment Options/Problems
Special! Free Choice of
Complete Excel Training Course
or Excel Add-ins Collection
on all purchases totaling over
$59.00.
ALL purchases totaling over $150.00 gets you BOTH! Purchases MUST be made via this site. Send payment proof to [email protected] 31 days after purchase date.
Instant Download and Money Back Guarantee on Most Software
Excel Trader Package Technical Analysis in Excel With $139.00 of FREE software!
Microsoft � and Microsoft Excel � are registered trademarks of Microsoft Corporation. OzGrid is in no way associated with Microsoft